The international standards for accrediting laboratory’s technical competence has evolved over the past 30 over years, started from ISO Guide 25: 1982 to ISO Guide 25:1990, to ISO 17025:1999, to ISO 17025:2005 and now to the final draft international standard FDIS 17025:2017, which is due to be published before the end of this year to replace the 2005 version. We do not anticipate much changes to the contents other than any editorial amendments.
The new draft standard aims to align its structure and contents with other recently revised ISO standards, and the ISO 9001:2015 in particular. It is reinforcing a process-based model and focuses on outcomes rather than prescriptive requirements such as eliminating familiar terms like quality manual, quality manager, etc. and giving less description on other documentation. It attempts to introduce more flexibility for laboratory operation.
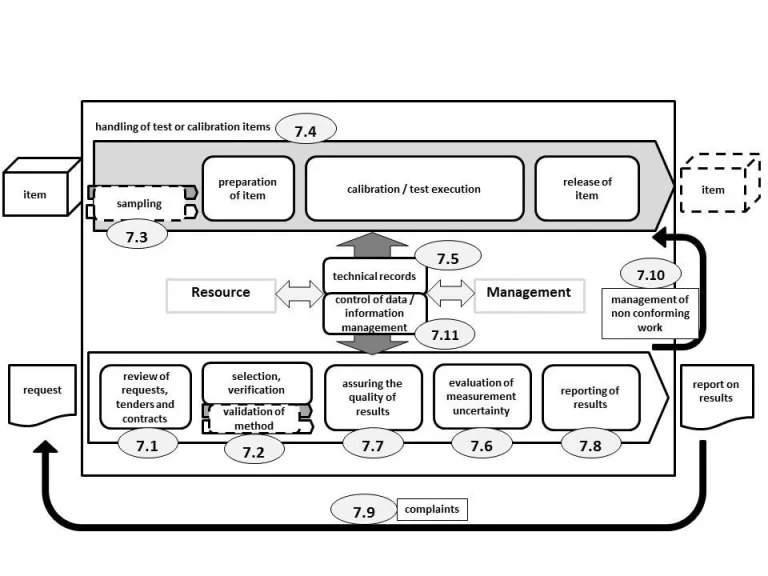
Although many requirements remain unchanged but appear in different places of the document, it has added some new concepts such as:
measurement uncertainty.
The purpose of introducing sampling as another activity is understandable, as we know that the reliability of test results is hanged on how representative the sample drawn from the field is. The saying test result is no better than the sample that it is based upon” is very true indeed.
If an accredited laboratory’s routine activity is also involved in the field sampling before carrying out laboratory analysis on the sample(s) drawn, the laboratory must show evidence of a robust sampling plan to start with, and to evaluate the associated sampling uncertainty.
It is reckoned however that in the process of carrying out analysis, the laboratory has to carry out sub-sampling of the sample received and this is to be part of the SOP which must devote a section on how to sub-sample it. If the sample received is not homogeneous, a consideration of sampling uncertainty is to be taken into account.
Although FDIS states that when evaluating the measurement uncertainty (MU), all components which are of significance in the given situation shall be identified and taken into account using appropriate methods of analysis, its Clause 7.6.3 Note 2 further states that “for a particular method where the measurement uncertainty of the results has been established and verified, there is no need to evaluate measurement uncertainty for each result if it can demonstrate that the identified critical influencing factors are under control”.
To me, it means that all identified critical uncertainty influencing factors must be continually monitored. This will have a pressured work load for the laboratory concerned to keep track with many contributing components over time if the GUM method is used to evaluate its MU.
The main advantage of the top down MU evaluation approach based on holistic method performance using the daily routine quality control data, such as intermediate precision and bias estimation is also appreciated as stated in Clause 7.6.3. Its Note 3 refers to the ISO 21748 which uses accuracy, precision and trueness as the budgets for evaluation of MU, as an information reference.
Secondly, this clause in the FDIS suggests that once you have established an uncertainty of a result by the test method, you can estimate the MU of all test results in a predefined range through the use of relative uncertainty calculation.
.webp)
Linear calibration curve – two common mistakes
Generally speaking, linear regression is used to establish or confirm a relationship between two variables. In analytical chemistry, it is commonly used in the construction of calibration functions required for techniques such as GC, HPLC, AAS, UV-Visible spectrometry, etc., where a linear relationship is expected between the instrument response (dependent variable) and the concentration of the analyte of interest.
The word ‘dependent variable’ is used for the instrument response because the value of the response is dependent on the value of concentration. The dependent variable is conventionally plotted on the y-axis of the graph (scatter plot) and the known analyte concentration (independent variable) on x-axis, to see whether a relationship exists between these two variables.
In chemical analysis, a confirmation of such relationship between these two variables is essential and this can be establish in terms of an equation. The other aspects of the calibration can then be proceeded.
The general equation which describes a fitted straight line can be written as:
y = a + bx
where b is the gradient of the line and a, its intercept with the y-axis. The least-squares linear regression method is normally used to establish the values of a and b. The ‘best fit’ line obtained from the squares linear regression is the line which minimizes the sum of the squared differences between the observed (or experimental) and line-fitted values for y.
The signed difference between an observed value (y) and the fitted value (ŷ) is known as a residual. The most common form of regression is of y on x. This comes with an important assumption, i.e. the x values are known exactly without uncertainty and the only error occurs in the measurement of y.
Two mistakes are so common in routine application of linear regression that it is worth describing them so that they can be well avoided:
Some instrument software allows a regression to be forced through zero (for example, by specifying removal of the intercept or ticking a “Constant is ‘zero’ option”).
This is valid only with good evidence to support its use, for example, if it has been previously shown that y-the intercept is not significant after statistical analysis. Otherwise, interpolated values at the ends of the calibration range will be incorrect. It can be very serious near zero.
Sometimes it is argued that the point (x = 0, y = 0) should be included in the regression, usually on the grounds that y = 0 is an expected response at x = 0. This is actually a bad practice and not allowed at all. It seems that we simply cook up the data.
Adding an arbitrary point at (0,0) will cause the fitted line to be more closer to (0,0), making the line fit the data more poorly near zero and also making it more likely that a real non-zero intercept will go undetected (because the calculated y-intercept will be smaller).
The only circumstance in which a point (0,0) can be validly be added to the regression data set is when a standard at zero concentration has been included and the observed response is either zero or is too small to detect and can reasonably be interpreted as zero.
