

Today there is a dilemma for an ISO/IEC 17025 accredited laboratory service provider in issuing a statement of conformity with specification to the clients after testing, particularly when the analysis result of the test sample is close to the specified value with its upper or lower measurement uncertainty crossing over the limit. The laboratory manager has to decide on the level of risk he is willing to take in stating such conformity.
However, there are certain trades which buy goods and commodities with a given tolerance allowance against the buying specification. A good example is in the trading of granular or pelletized compound fertilizers which contain multiple primary nutrients (e.g. N, P, K) in each individual granule. A buyer usually allows some permissible 2- 5% tolerance on the buying specification as a lower limit to the declared value to allow variation in the manufacturing process. Some government departments of agriculture even allow up to a lower 10% tolerance limit in their procurement of compound fertilizers which will be re-sold to their farmers with a discount.
Given the permissible lower tolerance limit, the fertilizer buyer has taken his own risk of receiving a consignment that might be below his buying specification. This is rightly pointed out in the Eurolab’s Technical Report No. 01/2017 “Decision rule applied to conformity assessment” that by giving a tolerance limit above the upper specification limit, or below the lower specification limit, we can classify this as the customer’s or consumer’s risk. In hypothesis testing context, we say this is a type II (beta-) error.
What will be the decision rule of test laboratory in issuing its conformity statement under such situation?
Let’s discuss this through an example.
A government procurement department purchased a consignment of 3000 bags of granular compound fertilizer with a guarantee of available plant nutrients expressed as a percentage by weight in it, e.g. a NPK of 15-15-15 marking on its bag indicates the presence of 15% nitrogen (N), 15% phosphorus (P2O5) and 15% potash (K2O) nutrients. Representative samples were drawn and analyzed in its own fertilizer laboratory.
In the case of potash (K2O) content of 15% w/w, a permissible tolerance limit of 13.5% w/w is stated in the tender document, indicating that a fertilizer chemist can declare conformity at this tolerance level. The successful supplier of the tender will be charged a calculated fee for any specification non-conformity
Our conventional approach of decision rules has been based on the comparison of single or interval of conformity limits with single measurement results. Today, we have realized that each test result has its own measurement variability, normally expressed as measurement uncertainty with 95% confidence level.
Therefore, it is obvious that the conventional approach of stating conformity based on a single measurement result has exposed the laboratory to a 50% risk of having the true (actual) value of test parameter falling outside the given tolerance limit, rendering it to be non-conformance! Is the 50% risk bearable by the test laboratory?
Let say the average test result of K2O content of this fertilizer sample was found to be 13.8+0.55%w/w. What is the critical value for us in deciding on conformity in this particular case with the usual 95% confidence level? Can we declare the result of 13.8%w/w found to be in conformity with specification referencing to its given tolerance limit of 13.5%w/w?
Let us first see how the critical value is estimated. In hypothesis testing, we make the following hypotheses:
Ho : Target tolerance value > 13.5%w/w
H1 : Target tolerance value < 13.5%w/w
Use the following equation with an assumption that the variation of the laboratory analysis result agrees with the normal or Gaussian probability distribution:
where
mu is the tolerance value for the specification, i.e. 13.5%,
x(bar) , the critical value with 95% confidence (alpha- = 0.05),
z, the z -score of -1.645 for H1’s one-tailed test, and
u, the standard uncertainty of the test, i.e. U/2 = 0.55/2 or 0.275
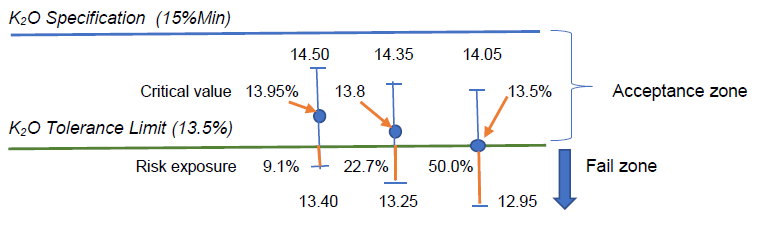
By calculation, we have the critical value x(bar) = 13.95%w/w, which, statistically speaking, was not significantly different from 13.5%w/w with 95% confidence.
Assuming the measurement uncertainty remains constant in this measurement region, such 13.95%w/w minus its lower uncertainty U of 0.55%w/w would give 13.40% which has (13.5-13.4) or 0.1%w/w K2O amount below the lower tolerance limit, thus exposing some 0.1/(2×0.55) or 9.1% risk.
When the reported test result of 13.8%w/w has an expanded U of 0.55%w/w, the range of measured values would be 13.25 to 14.35%w/w, indicating that there would be (13.50-13.25) or 0.25%w/w of K2O amount below the lower tolerance limit, thus exposing some 0.25/(2×0.55) or 22.7% risk in claiming conformity to the specification limit with reference to the tolerance limit given.
Visually, we can present these situations in the following sketch with U = 0.55%w/w:
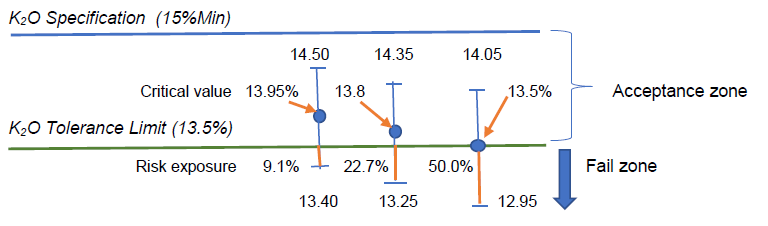
The fertilizer laboratory manager thus has to make an informed decision rule on what level of risk that can be bearable to make a statement of conformity. Even the critical value of 13.95%w/w estimated by the hypothesis testing has an exposure of 9.1% risk instead of the expected 5% error or risk. Why?
The reason is that the measurement uncertainty was traditionally evaluated by two-tailed (alpha- = 0.025) test under normal probability distribution with a coverage factor of 2 whilst the hypothesis testing was based on the one-tailed (alpha- = 0.05) test with a z-score of 1.645.
To reduce the risk of testing laboratory in issuing statement of conformity to zero, the laboratory manager may want to take a safe bet by setting his critical reporting value as (13.5%+0.55%) or 14.05%w/w so that its lower uncertainty value is exactly 13.5%w/w. Barring any evaluation error for its measurement uncertainty, this conservative approach will let the test laboratory to have practically zero risk in issuing its conformity statement.
It may be noted that the ISO/IEC 17025:2017 requires the laboratory to communicate with the customers and clearly spell out its decision rule with the clients before undertaking the analytical task. This is to avoid any unnecessary misunderstanding after issuance of test report with a statement of conformity or non-conformity.

By definition, sampling involves selecting a portion of material (i.e. sample or samples) from a substance, material, product or even a consignment of goods to represent or provide information about that larger body of material (i.e. population).
Although the ISO/IEC 17025 accreditation standards and also its latest revision are still concerned about the technical competence of organizations that conduct laboratory activities, it is reckoned that the reliability of testing result lies on how representative the sample analyzed is for the bulk material of interest. As the saying goes : “The result is not better than the sample that it is based on”.
A question has thus been asked: Can sampling be considered as a stand alone activity or should sampling activities always be associated with testing or calibration?
It is obvious that although the scope of this accreditation standards is with laboratory activities, sampling indeed has an inevitable connection to the laboratory’s analytical process that produces the test result which is important to the end users. It is usually impossible to analyze the whole bulk (or lot) of material (statistically called ‘population’ or ‘sampling target’). Therefore, proper sampling plays an essential role to ensure the validity of the final test result.
The FDIS requires laboratory to have a sampling plan and documented procedures for sampling in their field of testing. The laboratory is allowed to state “analyzed as received” in the report if it has not been responsible for the sampling stage. Also, laboratory performing sampling or testing activities shall evaluate measurement uncertainty, i.e. the uncertainty of sampling process is to be evaluated and forms an additional uncertainty contributor to the measurement uncertainty evaluation of the whole testing or calibration process.
Even though a laboratory does not get involved in the sampling of a population outside its premises, it often carries out sub-sampling process before the start of the analytical procedure. Therefore the subject of sampling cannot be ignored also in such laboratory.
As said earlier, since the main purpose of laboratory analysis is to estimate the value of analyte concentration in a sampling target, sample taken should be as representative of the sampling target under study as possible. This is to ensure that the property that each sample has the same probability of being drawn from the population as another sample.
So, in order to optimize the whole measurement process including taking a good sample for analysis, the sampling planner needs to gather information of the sampling target and to decide on appropriate sampling protocols.
Ask the following questions during information gathering:
To decide on the appropriate sampling protocols, one must try to deal with the following subjects:
We shall discuss these sampling strategies in more details in the next blog.