

The revised ILAC G8 document with reference to general guidelines on decision rules to issuance of a statement of conformance to a specification or compliance to regulatory limits has been recently published in September 2019. Being a guideline document, we can expect to be provided with various decision options for consideration but the final mode of application is entirely governed by our own decision with calculated risk in mind.
The Section 4.2 of the document gives a series of decision rules for consideration. In sub-section 4.2.1 which considers a binary statement (either pass or fail) for simple acceptance rule, it suggests a clear cut of test results to be given a pass or a fail without taking any risk of making a wrong decision into account, as long as the mean measured value falls inside the acceptance zone, as graphically shown in their Figure 3, whilst the reverse is also true:
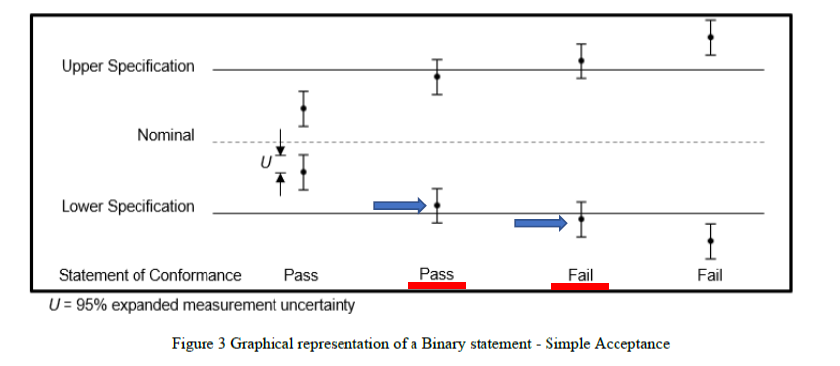
In this manner, my view is that the maximum risk that the laboratory is assuming when declaring conformity to a specification limit is 50% when the test result is on the dot of the specification limit. Would this be too high a risk for the test laboratory to take?
When guard bands (w) are used to reduce the probability of making an incorrect conformance decision by placing them between the upper and lower tolerance specification limit (TL) values so that the range between the upper and lower acceptance limits (AL) are narrower, we can simply let w = TL – AL = U where U is the expanded uncertainty of the measurement.
By doing so, we can have one of the two situations, namely for a binary statement, see Figure 4 of the ILAC G8 reproduced below and for a non-binary statement where multiple terms may be expressed, see Figure 5 of the ILAC document.
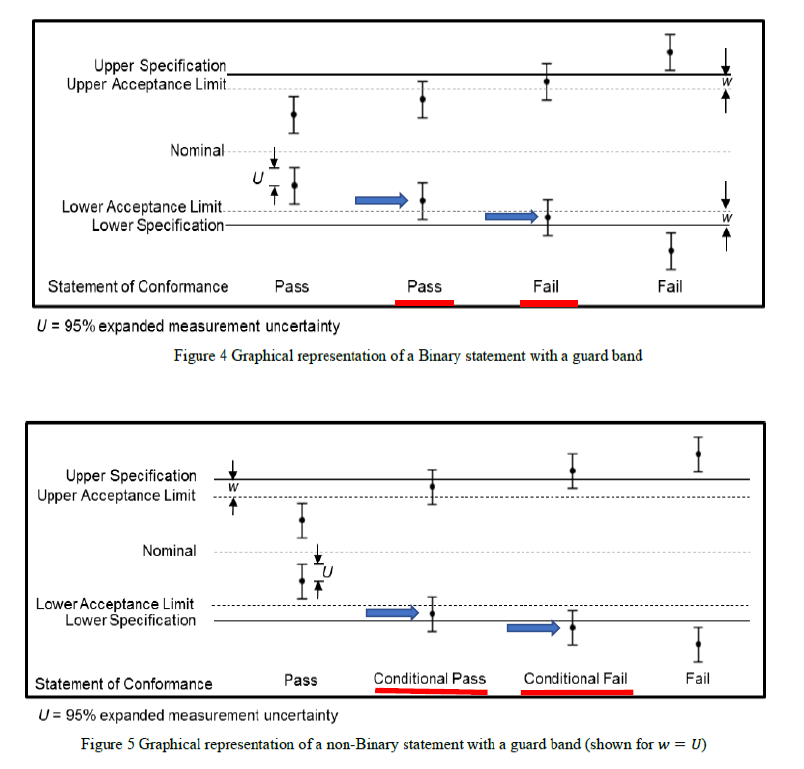

In my opinion, the decision to give a pass for the measurement found within the acceptance zone in Figure 4 is to the full advantage of the laboratory (zero risk as long as the laboratory is confident of its measurement uncertainty, U), but to state a clear “fail” in the case where the measurement is within the w-zone of the acceptance zone may not be received well by the customer who would expect a “pass” based on the numerical value alone, which has been done all this while. Shouldn’t the laboratory determine and bear a certain percentage of risk by working out with the customer on its acceptable critical measurement value where a certain portion of U lies outside the upper and lower specification limits?
Similarly, the “Conditional Pass / Fail” in Figure 5 also needs further clarification and explanations with the customer after considering a certain percentage of risk to be borne for the critical measurement values to be reported by the test laboratory. A statement to the effect that “a conditional pass / fail with 95% confidence” might be necessary to clarify the situation.
But from a commercial point of view, the local banker clearing a shipment’s letter of credit for payment with the requirement of a certificate of analysis to certify conformance to a quality specification laid down by the overseas buyer might not appreciate such statement format and might want to hold back the payment to the local exporter until his overseas principal agrees with this. Hence, it is advisable for the contracted laboratory service provider to explain and get written agreement with the local exporter on the decision rule in reporting conformity, so that the exporter in return can discuss such mode of reporting with the overseas buyers during the negotiation of a sales contract.
In my training workshops on decision rule for making statement of conformity after laboratory analysis of a product, some participants have found the subject of hypothesis testing rather abstract. But in my opinion, an understanding of the significance of type I and type II error in hypothesis testing does help to formulate decision rule based on acceptable risk to be taken by the laboratory in declaring if a product tested conforms with specification.
As we know well, a hypothesis is a statement that might, or might not, be true until we put it to some statistical tests. As an analogy, a graduate studying for a Ph.D. degree always carries out research works on a certain hypothesis given by his or her supervisor. Such hypothesis may or may not be proven true at the conclusion. Of course, a breakthrough of the research in hand means that the original hypothesis, called null hypothesis is not rejected.
In statistics, we set up the hypothesis in such as way that it is possible to calculate the probability (p) of the data, or the test statistic (such as Student’s t-tests) calculated from the data, given the hypothesis, and then to make a decision about whether this hypothesis is to be accepted (high p) or rejected (low p).
In conformity testing, we treat the specification or regulatory limit given as the ‘true’ or certified value and our measurement value obtained is the data for us to decide whether it conforms with the specification. Hence, our null hypothesis Ho can be put forward as that there is no real difference between the measurement and the specification. Any observed difference arises from random effects only.
To make decision rule on conformance in significance testing, a choice about the value of the probability below which the null hypothesis is rejected, and a significant difference concluded, must be made. This is the probability of making an error of judgement in the decision.
If the probability that the data are consistent with the null hypothesis Ho falls below a pre-determined low value (say, alpha = 0.05 or 0.01), then the hypothesis is rejected at that probability. Therefore, a p< 0.05 would mean that we reject Ho with 95% level of confidence (or 5% error) if the probability of the test statistic, given the truth of Ho, falls below 0.05. In other words, if Ho were indeed correct, less than 1 in 20 repeated experiments would fall outside the limits. Hence, when we reject Ho, we conclude that there was a significant difference between the measurement and the specification limit.
Gone are the days when we provide a conformance statement when the measurement result is exactly on the specification value. By doing so, we are exposed to a 50% risk of being found wrong. This is because we either have assumed zero uncertainty in our measurement (which cannot be true) or the specification value itself has encompassed its own uncertainty which again is not likely true.
Now, in our routine testing, we would have established the measurement uncertainty (MU) of test parameter such as contents of oil, moisture, protein, etc. Our MU as an expanded uncertainty has been evaluated by multiplying a coverage factor (normally k = 2) with the combined standard uncertainty estimated, with 95% confidence. Assuming the MU is constant in the range of values tested, we can easily determine the critical value that is not significantly different from the specification value or regulatory limit by the use of Student’s t-test. This is Case B in the Fig 1 below.
So, if the specification has an upper or maximum limit, any test value smaller than the critical value below the specification estimated by the Student’s t-test can be ‘safely’ claimed to be within specification (Case A). On the other hand, any test value larger than this critical value has reduced our confidence level in claiming within specification (Case C). Do you want to claim that the test value does not meet with the specification limit although numerically it is smaller than the specification limit? This is the dilemma that we are facing today.

The ILAC Guide G8:2009 has suggested to state “not possible to state compliance” in such situation. Certainly, the client is not going to be pleased about it as he has used to receive your positive compliance comments even when the measurement result is exactly on the dot of the upper limit.
That is why the ISO/IEC 17025:2017 standard has required the accredited laboratory personnel to discuss his decision rule with the clients and get their written consent in the manner of reporting.
To minimize this awkward situation, one remedy is to reduce your measurement uncertainty range as much as possible, pushing the critical value nearer to the specification value. However, there is always a limit to do so because uncertainty of measurement always exists. The critical reporting value is definitely going to be always smaller than the upper limit numerically in the above example.
Alternatively, you can discuss with the client and let him provide you his acceptance limits. In this case, your laboratory’s risk is minimized greatly as long as your reported value with its associated measurement uncertainty is well within the documented acceptance limit because your client has taken over the risk of errors in the product specification (i.e. customer risk).
Thirdly, you may want to take a certain calculated commercial risk by having the upper uncertainty limit extended into the fail zone above the upper specification limit, due to commercial reasons such as keeping good relationship with an important customer. You may even choose to report a measurement value that is exactly on the specification limit as conformance. However, by doing so, you are taking a 50% risk to be found err in the issued statement of conformance. Is it worth taking such a risk? Always remember the actual meaning of measurement uncertainty (MU) which is to provide a range of values around the reported number of the test, covering the true value of the test parameter with 95% confidence.
There are three fundamental types of risks associated with the uncertainty approach through making conformity or compliance decisions for tests which are based on meeting specification interval or regulatory limits. Conformity decision rules can then be applied accordingly.
In summary, they are:
1. Risk of false acceptance of a test result
2. Risk of false rejection of a test result
3. Shared risk
The basis of the decision rule is to determine an “Acceptance zone” and a “Rejection zone”, such that if the measurement result lies in the acceptance zone, the product is declared compliant, and, if it is in the rejection zone, it is declared non-compliant. Hence, a decision rule documents the method of determining the location of acceptance and rejection zones, ideally including the minimum acceptable level of the probability that the value of the targeted analyte lies within the specification limits.
A straight forward decision rule that is widely used today is in a situation where a measurement implies non-compliance with an upper or lower specification limit if the measured value exceeds the limit by its expanded uncertainty, U.
By adopting this approach, it should be emphasized that it is based on an assumption that the uncertainty of measurement is represented by a normal or Gaussian probability distribution function (PDF), which is consistent with the typical measurement results (being assumed the applicability of the Central Limit Theorem),
Current practices
When performing a measurement and subsequently making a statement of conformity, for example, in or out-of-specification to manufacturer’s specifications or Pass/Fail to a particular requirement, there can be only two possible outcomes:
Currently, the decision rule is often based on direct comparison of measurement value with the specification or regulatory limits. So, when the test result is found to be exactly on the dot of the specification, we would gladly state its conformity with the specification. The reason can be that these limits are deemed to have taken into account the measurement uncertainty (which is not normally true) or it has been assumed that the laboratory’s measurement value has zero uncertainty! But, by realizing the fact that there is always a presence of uncertainty in all measurements, we are actually taking a 50% risk to have the actual or true value of the test parameter found outside the specification. Do we really want to undertake such a high risky reporting? If not, how are we going to minimize our exposed risk in making such statement?